This article gives a set of information and methods on how to use the Cryptographic Library in a secure manner.
1. Cache-timing attack resistance
Timing attacks
Timing attacks specifically leverage differences in computational timings, in order to retrieve information on the private data used during the execution a cryptographic algorithm. Vulnerability to this class of attack is mainly due to:
- Conditional branches in the code, involving secret data
- Low-level machine instruction usage, the computational time of which depends on input data
- Compiler optimizations
Regular code execution
The solutions to avoid timing attacks are as follows:
- Develop regular code, running for the same time duration, independently from the input secret data.
- Break the correlation between secret input data and computational timing by randomizing the secret information, such that an attacker cannot recover the secret data from the retrieved randomized data.
Cache-timing attack (CTA)
Data leakage might occur even in a regular implementation, because of the presence of caches between the CPU and memory.
Caches are fast memories that are used to store frequently-used data; data loaded from the memory is stored in the cache before being passed to the CPU, and kept in the cache so that it can be quickly reloaded the next time it is requested.
Therefore, if data is in cache, the load is faster, whereas if the data is not in cache, the loading time is longer because information must be retrieved from main memory.
CTA exploit this property to steal secret data from regular algorithm implementations, where secret data is used as an index to access a memory location (for example a table).
Countermeasures against CTA
To avoid CTA, a real constant-time implementation must be developed.
In addition to regular code, correct management of the cache flow must always be considered.
Full parsing of tables
A possible countermeasure against these attacks is to avoid directly accessing the table using the secret data, but instead perform a loop-and-load on every single memory location in the table, and conditionally keep only the desired data.
The conditional test to check whether the current iteration is the desired one must be performed with regular code in order to avoid branches on secret data.
This way, the attacker cannot determine the secret index, because every possible index is used and every memory location is loaded, leading to a constant computation time.
The side effect of this countermeasure is a slight increase in computation time, due to the need of load every element of the table, instead of only the required value.
Use non-cacheable memories
Another solution to address caches vulnerability is to avoid the use of caches; often only flash memory is affected by cache. Sometimes however, faster memory than FLASH/SRAM is present in microcontroller, and this is not served by cache.
If these memories are big enough to keep the implementation tables, there is a double advantage in using:
- no vulnerability to CTA
- faster memory loading, resulting in faster computational timing
How to enable CTA resistance in the cryptographic library
The cryptographic library addresses CTA with constant-time code and uses non-cacheable memories.
The library already has linker labels associated to CTA-sensitive internal tables (usually residing in flash memory), the user only needs to map objects labeled with the label “CMOX_CTA_PROTECTED_DATA” onto the desired non-cacheable memory.
The example below shows how to create a linker script:
IAR Embedded Workbench: (Linker configuration file, .icf)
initialize by copy { readwrite, section CMOX_CTA_PROTECTED_DATA}; ... define region SAFEMEM_region = mem:[from 0x20030000 to 0x20034000]; ... place in SAFEMEM_region { section CMOX_CTA_PROTECTED_DATA };
Arm® KEIL µVision® IDE (Scatter file, .sct):
LR_IROM1 0x08000000 0x00200000 { ; load region size_region ... SAFEMEM 0x20030000 0x00004000 { *(CMOX_CTA_PROTECTED_DATA) } ... }
STM32CubeIDE (Linker script, .ld)
SECTIONS { ... user_SAFEMEM 0x20030000: { . = ALIGN(8); *(CMOX_CTA_PROTECTED_DATA) . = ALIGN(8); } ... }
In the linker file, add the highlighted lines, checking in your microcontroller manual for the correct non-cacheable memory start address and size. Note that the label SAFEMEM is a simple string decided by the user, and is not a specific value selected among a set of predefined values.
Depending on the microcontroller used, two scenarios could arise:
- Only Flash memory is affected by cache (for example ART caches): in this case no further operations are required to secure the implementation against CTA;
- SRAM is also affected by cache (for example L1 cache on STM32F7/H7). In this case, for ECC/RSA modules only where a temporary buffer is requested for internal computations, the user must also declare the temporary buffer as follows:
CMOX_CTA_RESISTANT uint8_t membuf[3000];instead of the standard way:
uint8_t membuf[3000];In order to use this macro, it is necessary to include the cmox_cta.h file, located in the root of the include folder.
2. Robust comparison (against simple faults)
Fault attacks
Faults events can occur on electronic devices. These have several possible causes, such as, too over/under temperature, unsupported supply voltage or current, strong electric or magnetic fields.
Fault attacks cause intentional faults on the device in order to influence the operation of the processor, with the purpose of retrieving secret information involved in the computation.
Simple faults
Simple fault attacks are the attack scenario that comprises a single fault, with limited possibilities:
- jump one or more consecutive instructions
- set a register (or a memory location) value to 0 or 0xFF…FFF
- flip every (or some) bits in a register (or a memory location)
What is robust comparison
Robust comparison is a strong way to check whether or not two buffers are equal, returning the appropriate comparison result (success or failure).
For example, even though a signature verification is securely implemented, an attacker could simply fault the final buffer comparison (or the comparison final result) in order to change the verification response to success.
How to enable robust comparison in the Cryptographic Library
To circumvent the above, a robust comparison is implemented, and every verification function in the library has a specific parameter (called P_pFaultCheck) to manage this.
The parameter is an optional pointer which can be NULL, if robustness against simple faults is not needed in the current scenario.
If instead, the parameter is provided to the verification function, the routine robustly checks against simple faults, returning not only the standard return value, but also filling the parameter variable with a second return value. This second return value must be checked against the main return value:
- If the main return value is FAIL, this means that the function correctly failed the verification, therefore there is no need to check the second return value.
- If the main return value is SUCCESS, this it means that the function correctly verified the inputs, or it did not detect a fault in the verification process. For this reason, it is necessary to check the second return value (the one inside the P_pFaultCheck parameter), by comparing it against the first return value:
- If it also has SUCCESS value, this means that the verification was really successful.
- otherwise, if it is different from the SUCCESS value, a fault was detected and the verification failed. Note that in the case of a fault, the second return value could be a dirty value, therefore the user must consider every value different from SUCCESS as a failure.
This robust comparison alone, however, is not sufficient to protect against simple faults.
Here in the code below example:
…
retval = cmox_rsa_pkcs1v15_verify(&rsa_ctx,
pub_key,
digest,
CMOX_RSA_PKCS1V15_HASH_SHA256,
signature,
sizeof(signature),
&fault_check);
if ((retval == CMOX_RSA_SUCCESS) && (fault_check == CMOX_RSA_SUCCESS))
{
return OK;
}
else
{
return FAIL;
}Here, an attacker could simply fault the conditional branch after the verification, in order to not take the failure branch, but instead take the success branch.
For this reason, it is important to securely check the two results of the robust verification process, as for example, in the code below:
…
retval = cmox_rsa_pkcs1v15_verify(&rsa_ctx,
pub_key,
digest,
CMOX_RSA_PKCS1V15_HASH_SHA256,
signature,
sizeof(signature),
&fault_check);
if (retval == CMOX_RSA_SUCCESS)
{
/* TODO: perform operations necessary to the final result of the developing functions */
…
if (fault_check == CMOX_RSA_SUCCESS)
{
return OK;
}
else
{
/* TODO: rollback previous operations computed after the first successful branch */
…
return FAIL;
}
}
else
{
return FAIL;
}In this case, an attacker could try to fault the program in order to directly jump to the OK return. However, this avoids the execution of the necessary operations (marked by the comment) the computation results in some error or segmentation fault, thwarting the successful attack.
With this new code, the attacker is forced to fault the computation twice, in the exact positions corresponding to the two branches, but this is beyond the scope of simple faults protections.
3. RSA countermeasures for Bellcore attack
Bellcore attack
The Bellcore attack is a fault attack that aims to recover the RSA private exponent by faulting one or more RSA computations (more specifically, the internal modular exponentiation), depending on the algorithm used.
To recover the private exponent of an RSA using CRT (Chinese remainder theorem) the attacker needs to fault just one operation, while for a standard RSA implementation, the attacker needs more faulted operations, all performed with certain criteria.
Therefore, in the cryptographic library it has been decided to protect the CRT implementation only.
Private operations in RSA are used both for decryption and signature creation. Since the Bellcore attack needs the output of the faulted operation, and a faulted decryption results in wrong padding causing the output to be filled with zeros, the RSA decryption processes do not need to be protected as the attacker is unable to get the faulted output.
Moreover, because of the algorithm itself, RSA PKCS#1 v2.2 is not vulnerable against the Bellcore attack, therefore only the RSA PKCS#1 v1.5 signature generation routine needs to be protected.
Countermeasure
For signature operations the countermeasure is simple; only verification of the signature validity is required before outputting it.
Signature verification (through the public key) is a very cheap operation with respect to the signature generation process, which therefore results in only a slight increase in the computation time.
For decryption, there is no high-level countermeasure, as the re-encryption of the decrypted message is non-deterministic (new random is used) and the values differ. However, as previously mentioned, since a faulted decryption would probably not have valid padding, the faulted decrypted message is not available to the attacker, thus negating the attack.
How to enable Bellcore attack countermeasures in the cryptographic library
To enable the countermeasure, instead of calling the standard way to set the CRT key:
cmox_rsa_retval_t cmox_rsa_setKeyCRT(cmox_rsa_key_t *P_pPrivKey,
size_t P_ModulusBitLen,
const uint8_t *P_pExpP,
size_t P_ExpPLen,
const uint8_t *P_pExpQ,
size_t P_ExpQLen,
const uint8_t *P_pP,
size_t P_PLen,
const uint8_t *P_pQ,
size_t P_QLen,
const uint8_t *P_pIq,
size_t P_IqLen);the user needs to call the following function:
cmox_rsa_retval_t cmox_rsa_setKeyCRTwithFACM(cmox_rsa_key_t *P_pPrivKey,
size_t P_ModulusBitLen,
const uint8_t *P_pExpP,
size_t P_ExpPLen,
const uint8_t *P_pExpQ,
size_t P_ExpQLen,
const uint8_t *P_pP,
size_t P_PLen,
const uint8_t *P_pQ,
size_t P_QLen,
const uint8_t *P_pIq,
size_t P_IqLen,
const uint8_t *P_pPubKey,
size_t P_PubKeyLen);(FACM stands for Fault attack countermeasures.) This requests the user to also provide the public key, in addition to the CRT private fields.
This call enables the countermeasures during the subsequent RSA computations, whose function calls remain the same.
4. RSA and the Bleichenbacher attack
Bleichenbacher attack in brief
When encrypting something with RSA PKCS#1 v1.5, the data that is to be encrypted is first padded, then the padded value is converted into an integer, and the RSA modular exponentiation (with the public exponent) is applied. Upon decryption, the modular exponentiation (with the private exponent) is applied, and then the padding is removed. The core of Bleichenbacher's attack relies on an oracle: the attack works if there is some system, somewhere, which can tell, given a sequence of bytes of the length of an encrypted message, whether decryption would yield something which has the proper padding format or not.
A real world example
An example could be a SSL/TLS server. In the initial handshake, at some point, the client is supposed to generate a random key (the "pre-master secret"), encrypt it with the server's public key, and send it. The server decrypts the value, obtains the pre-master secret, and then compute from it the key material used for the rest of the connection. The client sends a ClientKeyExchange (which contains the encrypted pre-master secret), then a ChangeCipherSpec, then Finished; this last message is encrypted with the derived symmetric key and its contents are verified by the server.
If the client sends a random sequence of bytes of the right length to the server instead of a properly encrypted pre-master secret, then the server, most of the time, responds with an error message telling "I tried to decrypt your ClientKeyExchange contents, but this failed, there was not a proper padding in it". However, by pure chance, it may happen that the random string, after applying the modular exponentiation, yields something which really looks like a pre-master secret with correct padding. In that case, the server does not complain about the ClientKeyExchange, but about the Finished message, which is incorrectly encrypted.
This is the information the attacker wants: whether the sequence of bytes he sent, upon decryption, looks properly padded or not.
PKCS#1 v1.5 padding details
In RSA, let n be the public modulus. Let M be a message to encrypt with n (in the case of SSL, M is the pre-master secret, of length 48 bytes). The PKCS#1 v1.5 padding, for encryption, consists in adding some bytes to the left, so that the total length after padding is equal to that of n. For instance, if the server's public key is a 2048-bit RSA key, then n has a length of 256 bytes, so the padded M must also have a length of 256 bytes.
A properly padded message M has the following format:
0x00 0x02 [some non-zero bytes] 0x00 [here goes M]The sequence of bytes begins with a byte of value 0, then a byte of value 2, then some bytes which should have random values (but not zero), then a byte of value 0, then M itself. The number of non-zero bytes is adjusted so that the total length is equal to the length of n. Upon decryption, the server looks at the first two bytes, and requires them to be equal to 0x00 and 0x02, in that order. Then it scans for the next byte of value 0, thus skipping over all the random non-zero bytes. This way, the padding can be unambiguously removed.
It follows that if the client sends a random string of bytes, then it has probability roughly between 2-15 and 2-17 to follow the PKCS#1 padding format (that's the probability that the first two bytes are 0x00 0x02, and that there is at least one byte of value 0 afterwards; exact probability depends on the length and value of n).
Attack details
There is a SSL server, which sends distinct error messages depending on whether a proper PKCS#1 padding was found or not. Alternatively, the two cases could be distinguished through some other information leak (e.g. the server takes longer to respond if the padding was correct).
The attacker eavesdropped on a connection, and would like to decrypt it. He observed the ClientKeyExchange, so he saw an encrypted message c. He knows that c=m•e (mod n) where e is the public exponent, and m is the padded pre-master secret for that connection. He wants to recover m, or at least the pre-master secret which is contained in m, because that allows him to compute the symmetric keys used for the connection.
Then the attacker initiates many connections to the server. For each connection, the attacker generates a value s and sends, as ClientKeyExchange, a value c′=c•se (mod n). The server decrypts that, and obtains m′=(c•se)d(mod n) (d is the private exponent), which is equal to m•s (mod n). Most of the time, this m•s value is not be properly padded (it does not begin with 0x00 0x02 or does not contain an extra 0x00). However, with a low but non-negligible probability (once every 30000 to 130000 attempts, roughly), luck will have it that the m•s (mod n) value looks padded. If that is the case, then the server's behavior informs the attacker of that fact. The attacker then learns that, for this value s (the attacker knows it, since he chose it), then m•s (mod n) is in a specific range (the range of integers which begin with 0x00 0x02 when encoded in bytes using big-endian convention).
The rest of the attack is trying again, with carefully chosen random values s. Each time the server responds with "that was a proper PKCS#1 padding", this gives some information which helps the attacker narrow his guesses on m. After a few million connections in all, the attacker learned enough to pinpoint the exact m, yielding the pre-master secret.
How to avoid the Bleichenbacher attack
This implementation of the RSA PKCS#1 v1.5 decryption in the STM32 Cryptographic library is constant-time and does not return a different return value error depending on the correct/incorrect padding. This, in order not to introduce the oracle needed by the Bleichenbacher attack. Nevertheless, the oracle can be introduced at a higher level in the application. To avoid this:
- Use the RSA PKCS#1 v2.2 correspondent functionality.
- If the PKCS#1 v1.5 version needs to be used (for example: for compatibility reasons), the SSL servers must not inform the client about padding woes. If decryption fails because of a bad padding, then the server must continue with a random pre-master secret in order to avoid the generation of the oracle (the true failure occurs when processing the Finished message).
5. Secure usage of random material
Why random material is so important
The strength of the random number generator used by a security system is rarely communicated, power consumption and bit generation speed being considered more important than the randomness of the generated bits.
This information is important however, considering that in most cryptographic systems, the quality of the random numbers used directly determines the security strength of the system.
The Kerckhoff principle states that the security of the system must depend solely on the key material, and not on the design of the system. This means that all modern security algorithms and protocols have their cryptographic strength expressed in the number of (key) bits that an attacker needs to guess before they can break the system (the actual definition of cryptographic strength is a measure of the complexity of a computational attack against the algorithm, often expressed as the log2 of the number of times attacker must invoke the algorithm before learning the value of the key used).
However, even if the key material for a cryptographic algorithm is not directly exposed, its generation from a bad source of randomness can compromise the overall security of the system. If there exists some sort of correlation among the “random” generated bits, an attacker can use statistical methods for deriving part or the whole key.
Some organizations, such as NIST, have defined statistical tests to be run on the output of a random number generator. Those tests should provide answers to some important problems, like determining how much unpredictability the random source generates, or how this unpredictability can be translated into random bits. The challenge is, however, that statistical tests cannot really prove that a source is random; at best, these tests can determine that a source is not, or is only partially, unpredictable.
It is in fact highly possible to create a module that creates a bit string that passes all the available statistical tests, but still generates a completely predictable bit stream, once the internal state of the module is known.
For this reason, standardization and certification organizations tend to require that a random number generator design is not tested by passing its output through a statistical test; rather, these organizations require that the design of the generator is reviewed, and its randomness generation properties explained and proven.
TRNG vs DRBG
A true random number generator (TRNG) is a device that generates random numbers from a physical process, and not by means of an algorithm. These devices are based on microscopic phenomena generating low-level, statistically random signals, such as thermal noise, photoelectric effect and other quantum phenomena. These stochastic processes are, in theory, completely unpredictable, and the theory's assertions of unpredictability are subject to experimental test.
A deterministic random bit generator (DRBG), or pseudorandom number generator (PRNG), is an algorithm that generates a sequence of numbers whose properties approximate those of sequences of true random numbers. The DRBG-generated sequence is not truly random, because it is completely determined by an initial value, called the DRBG's seed or entropy seed.
Although TRNGs are more secure than DRBGs, the latter are very important for several reasons:
- As long as a DRBG’s internal state is unknown to an attacker, the output it generates is unpredictable by the attacker.
- A well-constructed DRBG only leaks a limited amount of data about its internal state through the output it produces. Therefore, as long as the DRBG’s internal state is refreshed by new unpredictable data (that is, the DRBG is reseeded) often enough, its output remains unpredictable.
- Once a DRBG is properly seeded, it is extremely fast in terms of unpredictable output generation, compared to a TRNG.
How to get entropy from the STM32
TRNG peripheral
Most STM32 microcontrollers include a TRNG peripheral, and the HAL/LL drivers provide an API to generate true random numbers, 32 bits at a time. Refer to the driver documentation.
Entropy without a TRNG
When dealing with security in microcontrollers, it is always preferable to choose a device that includes a TRNG peripheral. However, not all the available STM32 MCUs provide such peripherals and, in this case, it is possible to exploit some sources of randomness from other components of the microcontroller.
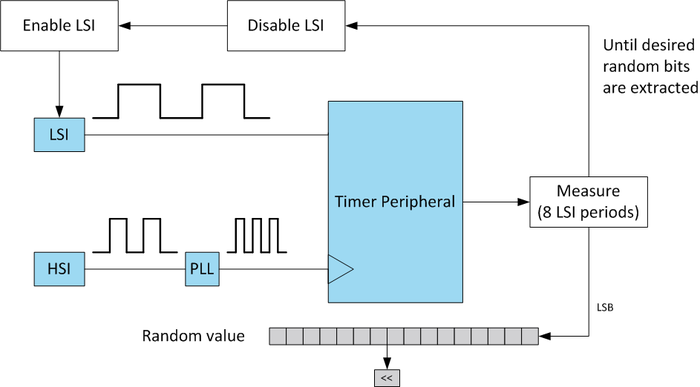
As an example, all STM32 MCUs provide two internal oscillators that can be used as clock sources: the HSI (high- speed internal) and the LSI (low-speed internal) oscillators. These two clock sources are not as accurate as crystal oscillators, in particular at startup time. Furthermore, the two sources are independent of each other and have different frequencies (for example in the STM32F401 the HSI frequency is ~16 MHz, while the LSI frequency is ~32 kHz, varying from 17 to 47). This can be exploited for generating some sort of randomness that can be used to seed a DRBG.
In the example shown above, a timer peripheral is configured with the HSI as clock source, and it is used to measure the LSI periods. In this way it is possible to check how many times an HSI period is included into an LSI one, and since both provide some uncertainty, the least significant bits of each measure are different to each other. For best results follow these recommendations:
- Restart the LSI oscillator at each measurement. This is because after the startup phase the oscillator becomes stable at a certain frequency. Restarting it changes the new stable frequency.
- Increase the timer clock source using the PLL together with the HSI oscillator. In this way the randomness measure from the LSI is more precise.
- It is possible to increase the timer prescaler in order to generate better random bits, at the cost of increasing the required time. In the above picture, the prescaler is set to 8, meaning that any measure takes 8 LSI periods.
- The best result is reached if, from any measure, only the least significant bit (LSB) is extracted. This means that in order to generate N random bits, N measurements are needed.
How to securely initialize the DRBG
Deterministic random bit generators (DRBGs) are based on cryptographic operations; for example, the ctrDRBG algorithm is based on the AES block cipher.
Before the DRBG is used for generate random material, it must be initialized with a seed. This operation determines the initial state of the DRBG.
It is also possible to periodically reseed the DRBG in order to make the random material generation stronger over time.
The initial seed is comprises three fields:
- An entropy input that must be generated by a reliable source of randomness (for example TRNG), and must be kept secret, otherwise the security of the DRBG is compromised. The security of the DRBG is highly dependent on the security strength of the randomness source used for the entropy generation.
- A nonce, the value of which is not expected to repeat during new instantiations. It does not need to be secret.
- A personalization string that is optional but recommended, which is used to integrate some additional information into the instantiation of the DRBG. It does not need to be secret.
Some DRBG implementations provide a derivation function that is used internally to derive a more secure seed from the given seeding materials. This means that with these implementations, it is possible to provide a non full-entropy input that is larger than the requested security strength, without compromising the overall security of the DRBG.
The seed used for reseeding is based on:
- the current internal state value of the DRBG
- a new entropy input
- an optional additional input
The cryptographic library provides an implementation of the ctrDRBG algorithm with a derivation function, which is specified in the NIST Special Publication 800-90A, together with other DRBG algorithms.
How to manage random material for ECC/RSA
The cryptographic library ECC/RSA APIs place on the user the responsibility for generating random bytes and providing them to the function call.
The random data may be generated not only with the library DRBG, but with a TRNG or other source preferred by the user.
Therefore, the cryptographic library functions ask the user for random bytes, and return a specific error if the provided data does not fulfil the requirements.
An effective way to manage random usage in the cryptographic library is to implement a loop in which random data is generated and the cryptographic function invoked, continuing iterating until no more random-related errors are returned by the cryptographic function.
Example with RSA:
cmox_rsa_retval_t rv; /* CLv4 return value */
uint8_t random_data[256]; /* array that will be filled with random bytes */
/* generate random until it's valid for RSA encryption function */
do
{
/* ToDo: fill 'random_data' with bytes generated by a specific source (DRBG, TRNG, etc.) */
...
/* call the RSA encryption function */
rv = cmox_rsa_pkcs1v15_encrypt(..., random_data, sizeof(random_data), ...);
}
while (rv == CMOX_RSA_ERR_WRONG_RANDOM);Necessary random material for ECC API
Some ECC functionalities need random material in order to process.
In particular, the following services need a random-bytes vector as input, and this byte array needs to be at least long as the chosen curve N parameter byte length (for example, 32 bytes for SECP256R1, 66 bytes for SECP521R1):
- ECDSA key generation
- ECDSA signature generation
- SM2 key generation
- SM2 signature generation
Even if the random array has the correct length, a failure might occur with return value CMOX_ECC_ERR_WRONG_RANDOM. A security check is done inside the ECC functions, assuring not only that the byte length is correct, but also that the value is compatible with the chosen curve N parameter.
For NIST curves, that have the N parameter starting with 0xFFFFFFFF…, this scenario is highly improbable, while for other curves (for example brainpoolP384r1) the probability can almost reach 50%.
The solution to this is to generate a new random byte array and recall the cryptographic API.
Necessary random material for RSA API
Some RSA functionalities need random material in order to process.
In particular, the following services need a random byte vector as input:
- RSA PKCS#1 v1.5 Encryption
- The array must contain at least (ModulusLength - InputLength - 3) not NULL bytes (that is, 0x00).
- Only that number of bytes is used if no NULL bytes (that is, 0x00) are in the sequence, otherwise more bytes are necessary to replace the NULL bytes.
- RSA PKCS#1 v2.2 Signature Generation
- The array length must be ≤ ModulusLength - HashLength - 2, where HashLength is the byte length of the digest generated by the chosen hash function.
- All the given bytes are processed and used inside an internal hashing process.
- RSA PKCS#1 v2.2 Encryption
- The array length must be ≥ HashLength, where HashLength is the byte length of the digest generated by the chosen hash function.
- Only HashLength bytes are used, while the others are discarded.
6. References
[TIMING-KOC96] P. Kocher, “Timing Attacks on Implementations of Diffie-Hellman, RSA, DSS, and Other Systems”, CRYPTO 1996
[FAULT-BDL97] D. Boneh, R. DeMillo, R. Lipton, “On the importance of checking cryptographic protocols for faults”, CRYPTO 1997
[BELLCORE-BDL01] D. Boneh, R. DeMillo, R. Lipton, “On the Importance of Eliminating Errors in Cryptographic Computations”, Journal of Cryptology 14(2), 2001
RND-RFC4086 Randomness Requirements for Security
RND-NIST.SP.800-90B Recommendation for the Entropy Sources Used for Random Bit Generation